Come funziona un neurone di una rete neurale
Di Nanni Bassetti – nannibassetti.com
Se prima volete leggere un mio articolo sul machine learning, algoritmi genetici e digital forensics cliccate qui:
https://www.cybersecurity360.it/soluzioni-aziendali/algoritmi-genetici-e-machine-learning-nella-digital-forensics-applicazioni-pratiche/
Il neurone descritto è quello più comune a livello didattico.
Pensiamo ad un oggetto non presente nel dataset, ossia l’insieme di oggetti dati in pasto alla rete neurale, che è definito da due input numerici, che chiamiamo X1 ed X2 questi input sono collegati al neurone tramite delle sinapsi (utilizziamo il paragone con la natura), che però non hanno tutte gli stessi valori, quindi saranno variabili e casuali, nel caso informatico chiameremo questi valori sinaptici, pesi (weights), quindi li indichiamo come w1 e w2.
Il neurone si attiva tramite una funzione d’attivazione, che chiamerò P(x1,x2) = x1*w1 + x2*w2 + b dove w1 e w2 sono dei pesi random (le connessioni tra gli X ed il neurone) e b è un numero chiamato bias.
Questa funzione serve a determinare il totale degli input che il neurone riceve e poi generare un output numerico.
La funzione P in realtà è:
Al fine di migliorare la scelta dei parametri w1,w2 e b, si deve introdurre una funzione di costo o Loss Function, che valuterà l’errore tra la previsione ed il risultato atteso e cercherà di minimizzarlo, questo avverrà tramite il calcolo dell’errore quadratico medio o mean square error (mse), dato da somma((previsione – output)^2 )/n
ESEMPIO:
L’ERRORE totale sarebbe -2+2 = 0, ma se eleviamo al quadrato i singoli errori avremmo 4 e 4 con un errore di 8, l’elevamento al quadrato ci evita di azzerare o valutare male l’errore totale, causato da errori negativi e positivi.
Il ricalcolo per ogni singolo parametro (w1, w2 e b) al fine di minimizzare la funzione di costo, si calcolerà così:
prima si calcola l’errore totale dato dalla formula precedente:
Poi ricalcoliamo w1, w2 e b utilizzando la formula:
LR è il Learning Rate un valore che non deve essere troppo grande o troppo piccolo che ci fornisce la velocità del calcolo e la convergenza verso la ricerca dell’errore minimo.
Se il learning rate è troppo piccolo il processo può diventare molto lento, se troppo grande potrebbe generare numeri troppo grandi, che non fanno convergere su un minimo per ridurre l’errore.
Mentre dE/dw1 è la derivata parziale della funzione di costo (Errore totale) rispetto a w1 e così si fa anche per w2 e per b.
Il ricalcolo dei pesi e del bias si chiama back propagation.
Grazie a questo meccanismo il valore dei pesi e del bias sarà sempre più preciso al fine di rendere la funzione di costo più piccola e quindi far coincidere il valore previsto con quello di output.
Con questo sistema, la rete neurale è in grado di imparare e classificare al meglio un oggetto in input.
Quindi in sintesi gli input vanno nel neurone che calcola la previsione forward propagation, poi si ricalcolano i parametri w1,w2 e b, per minimizzare la funzione di costo, quindi avvicinarci alla previsione (back propagation), alla fine questo avanti ed indietro trova la miglior previsione e la rete impara.






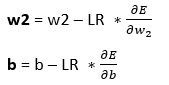
Commenti